Infer.NET user guide : Tutorials and examples
Page 1 | Page 2 | Page 3 | Page 4
Bayes Point Machine
The Bayes Point Machine, as implemented in this example, is represented by the following factor graph:
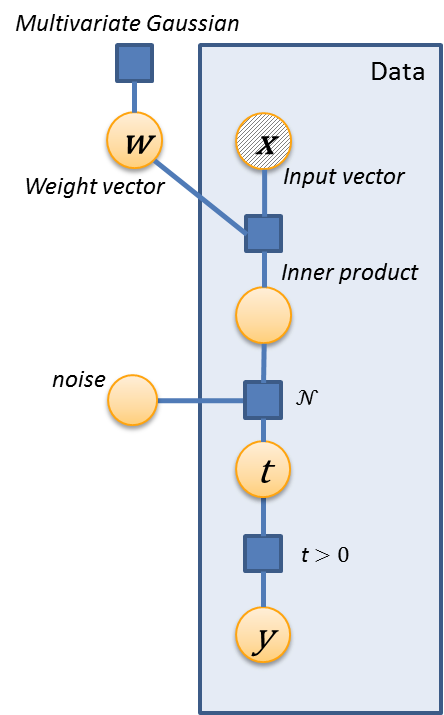
w is a vector Gaussian variable having prior with a multivariate Gaussian prior. For each data point, t is a latent variable formed by the inner product of w with the corresponding feature vector x. Adding noise then gives the latent variable y which is thresholded at 0 to produce a true ( ≥ 0) or false (< 0) answer which we observe during training.
This model is easily implemented in Infer.NET with the following C# code found in the constructor method for the BayesPointMachine class.
// Training model
nTrain = Variable.New<int>().Named("nTrain");
Range trainItem = new Range(nTrain);
trainingLabels = Variable.Array<bool>(trainItem).Named("trainingLabels");
trainingItems = Variable.Array<Vector>(trainItem).Named("trainingItems");
weights = Variable.Random(new VectorGaussian(new Vector(nFeatures),
PositiveDefiniteMatrix.Identity(nFeatures))).Named("weights");
trainingLabels[trainItem] = Variable.IsPositive(
Variable.GaussianFromMeanAndVariance(
Variable.InnerProduct(weights, trainingItems[trainItem]), noise));
The variables themselves are members of the BayesPointMachine class. nTrain, which corresponds to N (the number of data points), is also specified as a variable, but the setting of its observed value is deferred until run-time.
trainItem is a locally defined Range object - a range allows you to express repeated identical parts of your model in a succinct way. Often (as in this case) ranges are used to index data points in our training set.
trainingLabels(type VariableArray<bool>) and trainingItems(type VariableArray<Vector>) are, respectively, the observed output labels l and feature vectors x for our data set . As with nTrain, we defer setting these labels and feature vectors until run-time.
weights is the weight vector w which is defined with a prior having zero mean and identity positive definite precision matrix. If we wanted to be more general, we could make this prior a given in our model and pass down the mean vector m and precision matrix p. We write the factor as if we were taking a random sample from this prior distribution. The goal of the inference will be to infer the posterior distribution of w based on the observations.
The final line in this model definition combines the InnerProduct factor, the Gaussian noise factor, and the IsPositive factor into one expression, the result of which is then equated to the observation. Unraveling this from the innermost expression, we see that first we apply the Variable.InnerProduct method to get the latent variable t, we then apply the Variable.GaussianFromMeanAndVariance method to define the noisy latent variable y, whose sign is computed by Variable.IsPositive. The resulting implicit bool random variable is then equated to the observation. There are several points to note in this last step:
- The
trainItemrange allows for a very succinct statement that the expression is repeated for all indices in the range. - weights is not indexed by
trainItembecause there is only one copy of w across all data points - t and y are implicit in the final expression. You can, of course, split up the expression - either for reasons of clarity, or if you want to recover their posteriors.
- noise is a parameter passed down to the BayesPointMachine constructor, and so it is hard-wired into a particular instance of the model.
In preparation for inference, our BayesPointMachine constructor also creates an inference engine which contains the inference parameters we want to use for training:
trainEngine = new InferenceEngine(new ExpectationPropagation());
trainEngine.NumberOfIterations = 5;
We specify that we want to use Expectation Propagation as our algorithm, and that we only want to do 5 passes through the data when learning the weight posteriors (experience with these types of models shows that this is usually sufficient).
