Infer.NET user guide

The Infer.NET Modelling API

When using Infer.NET, you first define a probabilistic model to work with. If you don’t know what a probabilistic model is, or just need a refresher, take a look at Resources and References. The Modelling API (Application Programming Interface) allows you to create model variables and observations, and specify how these relate to each other. To use the modelling API, you must import the Microsoft.ML.Probabilistic.Models namespace.

Here is a simple example of using the modelling API to define a model for learning the mean and precision (inverse variance) of a Gaussian:

Variable<double> mean = Variable.GaussianFromMeanAndVariance(0, 100);  
Variable<double> precision = Variable.GammaFromShapeAndScale(1, 1);  
VariableArray<double> data = Variable.Constant(new double[] { 11, 5, 8, 9 });  
Range i = data.Range;  
data[i] = Variable.GaussianFromMeanAndPrecision(mean, precision).ForEach(i);

The factor graph for this model is shown below.

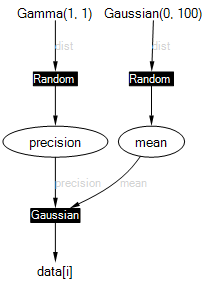
This example creates two random variables, mean and precision with Gaussian and Gamma priors. It also creates a constant array data; ‘constant’ here means that the values in this array will be compiled into the model and will not be changeable when we run the model. The range i ranges across the data indices from 0 to 3. The final line ties all of the above together by constraining the data points to be drawn from a Gaussian with mean mean and precision precision. Overall, this model provides a way to learn posterior distributions over the mean and precision of some data. To see how to run inference in this model, see running inference.

You can see from this example that the modelling API is accessed almost entirely through static methods on the Variable class. The following pages describe how various modelling tasks can be achieved using the modelling API:

• Creating variables
  • Variable types and their distributions
  • Vector and Matrix types
  • Applying functions and operators to variables
• Attaching constraints to variables
• Working with arrays and ranges
  • Arrays and ranges
  • ForEach blocks
  • Markov chains and grids
  • Jagged arrays
  • Indexing arrays by observed variables
  • Cloning ranges
• Branching on variables to create mixture models
  • The importance of using SetTo
• Repeat blocks
• Computing model evidence for model selection
• Increment log density

Finally, note that the use of Variable.Constant() is a convenience for the early stages of model development. For efficiency, scalability, and flexibility, it is preferable the Observed value mechanism as described in Creating variables.