Learners : Matchbox recommender : Learner API : Evaluation

Rating prediction

There are two types of rating prediction supported for evaluation - exact rating prediction (when the predictions are point estimates) and uncertain rating prediction (when the predictions are discrete distributions over the rating values).

Evaluating exact rating prediction

Exact rating predictions are produced when the Predict method of the IRecommender interface is used. The evaluator currently supports three metrics for such predictions:

• Absolute error - the absolute difference between the prediction and the ground truth
• Squared error - the squared difference between the prediction and the ground truth
• Zero-one error - 0 if the prediction and the ground truth are the same, 1 otherwise

These can be computed by calling into the RatingPredictionMetric method. It takes in a data source of the ground truth instances, the predictions, and the specified metric. The predictions are expected to be in the form returned by the bulk prediction method: IDictionary<TUser, IDictionary<TItem, TPredictedRating>>.

double rmse = Math.Sqrt(  
    evaluator.RatingPredictionMetric(groundTruth, predictions, Metrics.SquaredError));

Apart from the metrics defined in the Metrics enumeration, you can also define your own evaluation metric and pass it to RatingPredictionMetric. For example:

double mae = evaluator.RatingPredictionMetric(  
    groundTruth, predictions, (x, y) => Math.Abs(x - y));

The error metrics can also be computed in model domain. We distinguish between data domain - where the ratings can be of any type, and model domain - where the ratings are of an integer type (that is, they are assumed to be star ratings). The rating in model domain is obtained using the IStarRatingInfo object returned by the GetRatingInfo method from the data mapping. The model-domain metric computation is performed by the ModelDomainRatingPredictionMetric method, which has the same signature as the RatingPredictionMetric method:

double zoe = evaluator.ModelDomainRatingPredictionMetric(  
    groundTruth, predictions, groundTruth, predictions, Metrics.ZeroOneError);

Evaluating uncertain rating prediction

Uncertain rating predictions are produced when the PredictDistribution method of the IRecommender interface is used. They are only evaluated in model domain, because this is where the evaluator knows how to deal with the produced uncertainty. The metrics used are the same as above but now the evaluator method is called ModelDomainRatingPredictionMetricExpectation and it expects uncertain predictions as opposed to point estimates:

double expectedMae = evaluator.ModelDomainRatingPredictionMetricExpectation(  
    groundTruth, uncertainPredictions, Metrics.AbsoluteError);

The uncertain metrics compute the expectation under the rating posterior. This is implemented by iterating over the ratings and adding up the product of the predictive probability for this rating value and the metric computation for this rating value:

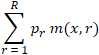
where r is the index of the current rating, x is the ground truth rating, m is the metric computation function, and p__r is the predictive probability for rating r.

Normalization per user

The default way the evaluator works is by iterating over all instances, adding up the computed errors for each instance, and finally dividing by the number of instances. This behaviour can be changed in case normalization by user is required. The alternative is to average the metric values per user first, then add them up for all users, and finally divide by the number of users. In order to control this, all methods listed above have an overload which takes a parameter of type RecommenderMetricAggregationMethod as a last argument. It can be either Default or PerUserFirst.

double normalizedPerUserMae = evaluator.RatingPredictionMetric(  
    groundTruth,  
    predictions, Metrics.AbsoluteError, RecommenderMetricAggregationMethod.PerUserFirst);

Confusion matrices

Often when evaluating rating prediction a useful summary of how well the model performs is the confusion matrix. It is implemented in the RatingMatrix class, and can be obtained for both exact and uncertain rating predictions:

RatingMatrix confusion = evaluator.ConfusionMatrix(  
    groundTruth, predictions, RecommenderMetricAggregationMethod.PerUserFirst);  
RatingMatrix expectedConfusion = evaluator.ExpectedConfusionMatrix(  
    groundTruth, uncertainPredictions);groundTruth, uncertainPredictions);

A component-wise product of the confusion matrix and a loss matrix gives the weighted confusion. A loss matrix can be specified using the RatingMatrix class and component-wise product can be computed using the ComponentwiseProduct static method of the same class:

double weightedConfusion = RatingMatrix.ComponentwiseProduct(confusionMatrix, lossMatrix);

For convenience, the evaluator provides methods for doing all of this in one go for both exact and uncertain predictions:

double weightedConfusion = evaluator.WeightedConfusion(groundTruth, predictions, lossMatrix);  
double expectedWeightedConfusion = evaluator.ExpectedWeightedConfusion(  
    groundTruth, uncertainPredictions, lossMatrix);

The RatingMatrix class also provides a number of pre-defined loss matrices - AbsoluteErrorLossMatrix, SquaredErrorLossMatrix, and ZeroOneErrorLossMatrix. For example,

evaluator.WeightedConfusion(  
    groundTruth,   
    predictions, RatingMatrix.AbsoluteErrorLossMatrix(minStarRating, maxStarRating))

is equal to

evaluator.ModelDomainRatingPredictionMetric(groundTruth, predictions, Metrics.AbsoluteError)